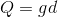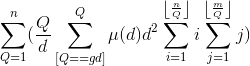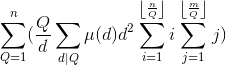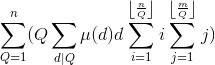This article is made by Jason-Cow.Welcome to reprint.But please post the article's address.
莫比乌斯定理(未完待续......):
形式1:
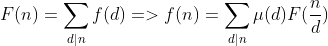
形式2:
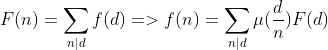
引理:

证明1:
右边=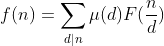 带入左边等式,得
带入左边等式,得
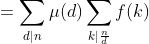
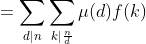

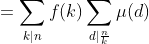 又
又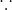
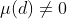 当且仅当 :
当且仅当 :  ,即
,即 时,上式非
时,上式非
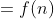
所以,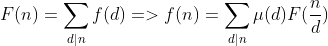 成立。
成立。
bzoj2154
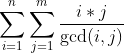
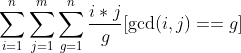
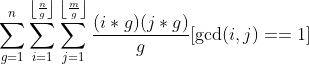
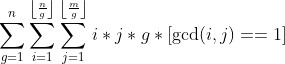

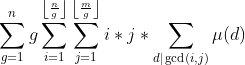

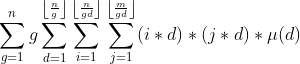
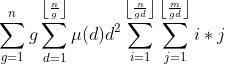
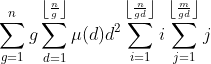
时间复杂度

换元:令
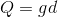
/*
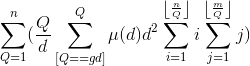
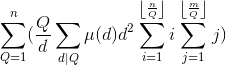
*/
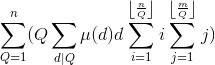
此题的精髓就一个字,模
1 #include 2 #include 3 #include 4 #include 5 #include 6 #include 7 #include 8 #include 9 #include
f(n)=∑d|nμ(d)F(nd)=∑d|nμ(d)∑k|ndf(k)=∑k|nf(k)∑d|nkμ(d)
带入左边等式,得
又
当且仅当 :
,即
时,上式非
成立。